Python Scipy Kdtree [With 10 Examples]

In this Python tutorial, we will learn about “Python Scipy Kdtree” where will learn how to find or search the nearest points of a specific point. Additionally, we will cover the following topics.

• What is KDtree
• Python Scipy Kdtree Query
• Python Scipy Kdtree Query Ball Point
• Python Scipy Kdtree Query Pairs
• Python Scipy Kdtree
• Python Scipy Kdtree Query Ball Tree
• Python Scipy Kdtree Count Neighbors
• Python Scipy Kdtree Sparse Distance Matrix
• Python Scipy Kdtree vs ckdtree
• Python Scipy Kdtree Leafsize
• Python Scipy Kdtree Slow

Before starting this tutorial makes sure Python and Scipy are installed. Here is a tutorial that can help: Installation of Scipy.

What is KDtree

A space-partitioning data structure known as a k-d tree (short for k-dimensional tree) is used in computer science to organize points in a k-dimensional space. K-d trees are a helpful data structure for many applications, including making point clouds and performing searches with a multidimensional search key (such as range searches and closest neighbor searches). A specific type of binary space partitioning tree is a k-d tree.

Read: Python Scipy Stats Kurtosis

Scipy Kdtree Query

The method KDTree.query() exists in a module scipy.spatial that finds the closest neighbors.

The syntax is given below.

KDTree.query(x, eps=0, k=1, p=2, workers=1, distance_upper_bound=inf,)

Where parameters are:

• x(array_data, last dimension): an array of queryable points.
• eps(nonnegative float): The kth reported result is guaranteed to be no more than (1+eps) times the distance to the actual kth nearest neighbor. Return approximate nearest neighbors.
• k(int, sequence int): A list of the kth nearest neighbors to return, starting with 1, or the number of nearest neighbors to return.
• p(float): Using which Minkowski p-norm. The sum-of-absolute-values (or “Manhattan”) distance is 1. The typical Euclidean distance is two. The distance with the greatest coordinate difference is infinity. If overflow is possible with a large, finite p, a ValueError may result.
• workers(int): Used for parallel processing in terms of workers. Every CPU thread is utilized if -1 is provided. By default: 1.
• distance_upper_bound(nonnegative float): Only those close by will be returned. It may be helpful to provide the distance to the most recent point’s nearest neighbor if you are performing a series of nearest-neighbor queries because this is used to reduce tree searches.

The method KDTree() returns d(The distance between the closest neighbors) and i(The neighbor’s index in self.data.i resemble d in form. Self.n is used to indicate missing neighbors) of type float and integers respectively.

Let’s take an example by following the below steps:

Import the required libraries using the below python code.

from scipy import spatial
import numpy as np

Create a multidimensional array and pass it to the KDTree using the below code.

x_data, y_data = np.mgrid[0:6, 2:7]
kd_tree = spatial.KDTree(np.c_[x_data.ravel(), y_data.ravel()])

Use the following code to do a squeezed neighbor search and get results:

d, i = kd_tree.query([[0, 0], [1.1, 1.9]], k=1)
print(d, i, sep='\n')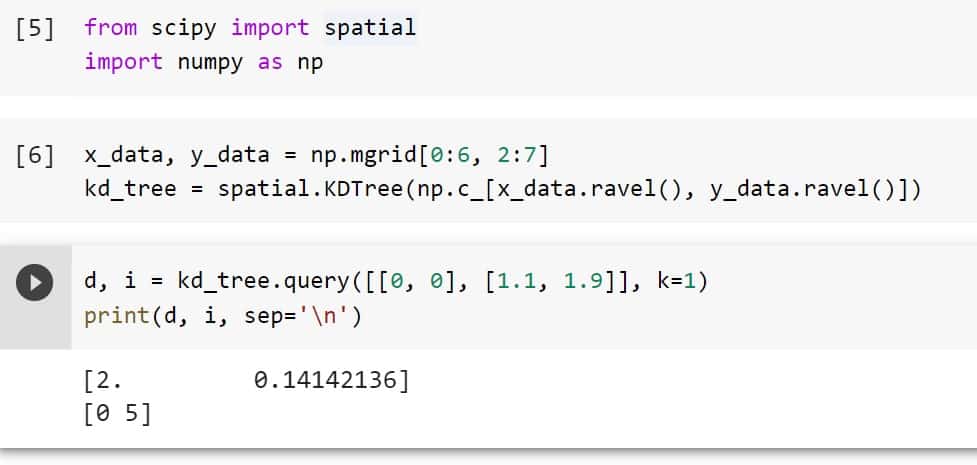

This is how to use the method KDTree.query() of Python Scipy to find the closest neighbors.

Read: Scipy Optimize 

Python Scipy Kdtree Query Ball Point

The method KDTree.query_ball_point() exists in a module scipy.spatial that find all points that are closer to point(s) x than r.

The syntax is given below.

KDTree.query_ball_point(x, r, p=2.0, eps=0, workers=1, return_sorted=None, return_length=False)

Where parameters are:

• x(array_data): Which point or points should be used to look for nearby points.
• r(array_data): The length of x must be broadcast by the radius of the points to return.
• p(float): Which Minkowski p-norm should be applied. Must fall between [1, inf]. If overflow is possible for a finite large p, a ValueError can result.
• eps(nonnegative float): Estimated search. The tree’s branches are not examined if their closest points are more than r / (1 + eps) away, and they are bulk-added if they are closer than r * (1 + eps).
• workers(int): Used for parallel processing in terms of workers. Every CPU thread is utilized if -1 is provided. By default: 1.
• return_sorted(boolean): If True, the returned indices are sorted; if False, they are not sorted. If None sorts multi-point queries instead of single-point searches, which was the default behavior before the addition of this option.
• return_length(boolean): Instead of a list of the indices, returns the total number of points within the radius.

The method query_ball_point() returns result, which is a list of the indices of x’s neighbors is returned if x is a single point. Returns a shape tuple object array with lists of neighbors if x is an array of points.

Let’s take an example by following the below steps:

Import the required libraries using the below python code.

from scipy import spatial
import numpy as np

Create a multidimensional array and pass it to the KDTree using the below code.

x_data, y_data = np.mgrid[0:7, 0:7]
kd_tree = spatial.KDTree(np.c_[x_data.ravel(), y_data.ravel()])

Pass the above data to the method query_ball_point() to find all points that are closer to point(s) x than r, using the below code.

sorted(kd_tree.query_ball_point([3, 1],2))

Read: Scipy Stats – Complete Guide

Python Scipy Kdtree Query Pairs

The method KDTree.query_pairs() exists in a module scipy.spatial Find all point pairings within self whose distances are r or less.

The syntax is given below.

KDTree.query_pairs(r, p=2.0, eps=0, output_type='set')

Where parameters are:

• r(positive float): It is the maximum distance.
• p(float): What Minkowski standard to apply. The constraint 1 = p <= infinity must be met by p.
• eps(nonnegative float): Estimated search. The tree’s branches are not examined if their closest points are more than r / (1 + eps) away, and they are bulk-added if they are closer than r * (1 + eps).
• output_type(string): Select either “set” or “ndarray” as the output container. By default : “set”

The method query_pairs() returns result of type set or ndarray, which is a group of pairs (i,j) where I > j and the corresponding places are near together. A ndarry is returned as opposed to a set if the output type is ‘ndarray’.

Let’s understand with an example by following the below steps:

Import the required libraries using the below python code.

import numpy as np
import matplotlib.pyplot as plt
from scipy import spatial

Generate data points using the random generator as shown in the below code.

rnd_gen = np.random.default_rng()
pts = rnd_gen.random((30, 3))

Pass the points to kdtree and find all point pairings within a r distance in a kd-tree using the below code.

kdtree = spatial.KDTree(pts)
prs = kdtree.query_pairs(r=0.3)

Plot the pairs using the below code.

plt.figure(figsize=(5, 5))
plt.plot(pts[:, 0], pts[:, 1], "xk", markersize=14)

for (i, j) in prs:
    plt.plot([pts[i, 0], pts[j, 0]],
            [pts[i, 1], pts[j, 1]], "-r")
plt.show()

Read: Scipy Integrate + Examples

Python Scipy Kdtree

The Python module scipy.spatial contains class KDTree() find the nearest neighbor quickly.

• Maneewongvatana and Mount 1999 describe the algorithm in detail. The kd-tree is conceptualized as a binary tree with each node denoting an axis-aligned hyperrectangle. Each node designates an axis and divides the set of points according to whether their coordinate along that axis exceeds or falls below a specific value.

The syntax is given below.

scipy.spatial.KDTree(data, leafsize=10, compact_nodes=True, copy_data=False, balanced_tree=True, boxsize=None)

Where parameters are:

• data(array): The n measurement points of dimension m that will be indexed. Since this array is not copied unless it is required to create a contiguous array of doubles, altering this data would yield false results. If copy data=True is specified when building the kd-tree, the data are also copied.
• leafsize(positive int): How many times the algorithm turns to brute-force methods Standard: 10.
• compact_nodes(boolean): If this is the case, the hyper rectangles are shrunk to fit the data range by the kd-tree. At the tradeoff of a longer build time, this typically results in a more compact tree that is resilient against degraded input data and provides faster queries. As a rule, yes.
• copy_data(boolean): If True, data is always replicated to guard against data corruption and safeguard the kd-tree. False by default.
• balanced_tree(boolean): If this is the case, the hyper rectangles are divided using the median rather than the midpoint. Usually, the trade-off for a longer build time is a more compact tree and quicker queries. As a rule, yes.
• boxsize(scalar, array_data): Give the KDTree an m-d toroidal topology. The topology is produced by where L i is the boxsize along the i-th dimension and n i are integers. The input data needs to be enclosed in [0, L i]. If any of the data is outside of this bound, a ValueError is raised.

Read: Scipy Find Peaks

Python Scipy Kdtree Query Ball Tree

The Python Scipy contains a method query_ball_tree() in a module scipy.spatial..KDTree that find every pair of points between self and another that is distanced by at most r.

The syntax is given below.

KDTree.query_ball_tree(other, r, p=1.0, eps=1)

Where parameters are:

• other(KDTree instance): The tree that contains search points.
• r(float): The maximum distance must be positive.
• p(float): What Minkowski norm to employ. The constraint 1 = p < infinity must be met by p.
• eps(nonnegative float): Estimated search. The tree’s branches are not examined if their closest points are more than r / (1 + eps) away, and they are bulk-added if they are closer than r * (1 + eps).

The method query_ball_tree() returns result of type list of list, where it returns results[i] is a list of the indices of the neighbors in other.data for each element of this tree with the self.data[i] prefix.

Let’s take an example by following the below steps:

Import the required libraries using the below python code.

import numpy as np
import matplotlib.pyplot as plt
from scipy import spatial

Generate data points using the random generator as shown in the below code.

rnd_gen = np.random.default_rng()
pts = rnd_gen.random((20, 3))
pts2 = rnd_gen.random((20,3))

Pass the points to kdtrees and find all point pairings within an r distance in a kd-tree using the below code.

kdtree = spatial.KDTree(pts)
kdtree2 = spatial.KDTree(pts2)
idx = kdtree.query_ball_tree(kdtree2, r=0.3)

Plot the pairs using the below code.

plt.figure(figsize=(5, 5))
plt.plot(pts[:, 0], pts[:, 1], "xk", markersize=14)
plt.plot(pts2[:, 0], pts2[:, 1], "og", markersize=14)

for i in range(len(idx)):
    for j in idx[i]:
        plt.plot([pts[i, 0], pts2[j, 0]],
            [pts[i, 1], pts2[j, 1]], "-r")
plt.show()

Read: Python Scipy Matrix + Examples

Python Scipy Kdtree Count Neighbors

The method count_neighbors() of Python Scipy that exists in the module scipy.spatial count the number of pairings that can form nearby.

Count the number of pairs (x1,x2) that may be constructed where distance(x1, x2, p) = r and where x1 is drawn from self and x2 is drawn from the other.

The syntax is given below.

KDTree.count_neighbors(other, r, p=1.0, weights=None, cumulative=False)

Where parameters are:

• other(KDTree): The second tree from which points are to be derived may be the first tree itself.
• r(float, 1d float): The radius within which to compute a count. One tree traversal is used to search across many radii. R determines the boundaries of the bins and must not decrease if the count is not cumulative (cumulative=False).
• p(float): 1<=p<=infinity. using which Minkowski p-norm. Standard 2.0 If overflow is possible, a finite large p can result in a ValueError.
• weights(array_data, tuple array): Pair counting is weightless if None. The weights of the points in oneself and the weights of the points in the other, if provided as a tuple, are weights[0] and weights[1, respectively].
• cumulative(boolean): Whether the counts that were returned are cumulative. The procedure is optimized to function with a large number of bins (>10) indicated by r when cumulative is set to False. The method is tuned to operate with a limited number of r when cumulative is set to True. By default: True

The method count_neighbors() returns result of type scalar or one-dimensional array which is the number of pairings. The outcome for unweighted counts is an integer. The outcome for weighted counts is float. Result[i] contains the numbers with (-inf if I == 0 else r[i-1]) if cumulative is False. < R <= r[i].

Let’s understand with an example by following the below steps:

Import the required libraries using the below python code.

import numpy as np
import matplotlib.pyplot as plt
from scipy import spatial

Generate data points using the random generator as shown in the below code.

rnd_gen = np.random.default_rng()
pts = rnd_gen.random((10, 2))
pts2 = rnd_gen.random((10,2))

Pass the points to kdtrees, and between two kd-trees, calculate the number of neighbors that are nearby using the below code.

kdtree = spatial.KDTree(pts)
kdtree2 = spatial.KDTree(pts2)
kdtree.count_neighbors(kdtree2, r=0.3)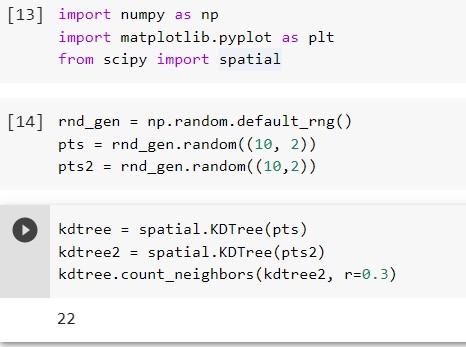

From the output, we can see that the number of neighbors between two kdtree is 22.

Read: Scipy Normal Distribution

Python Scipy Kdtree Sparse Distance Matrix

The method sparse_distance_matrix of module scipy.spatial.KDTree in Python Scipy calculates a matrix of distances between two KDTrees, leaving any distances more than the max distance as 0.

The syntax is given below.

KDTree.sparse_distance_matrix(other, max_distance, p=1.0, output_type='coo_matrix')

Where parameters are:

• other: It is KDTree.
• max_distance(positive float): It is used to specify maximum distance.
• p(float): 1<=p<=infinity. using which Minkowski p-norm. If overflow is possible, a finite large p can result in a ValueError.
• output_type(string): Which output data container to utilize. Options include “ndarray,” “dict,” “coo matrix.” and “dok matrix,”, ‘dok matrix’ is the default.

The method sparse_distance_matrix() returns result which is the sparse matrix displaying the outcomes as a “dictionary of keys” The keys of a returned dict are (i,j) tuples of indexes. An array of records with the fields I “j,” and “v” is returned if the output type is “ndarray.”

Let’s understand with an example by following the below steps:

Import the required libraries using the below python code.

import numpy as np
import matplotlib.pyplot as plt
from scipy import spatial

Generate data points using the random generator as shown in the below code.

rnd_gen = np.random.default_rng()
pts = rnd_gen.random((10, 4))
pts2 = rnd_gen.random((10,4))

Pass the points to kdtrees, and between two kd-trees, calculate a sparse distance matrix. using the below code.

kdtree = spatial.KDTree(pts)
kdtree2 = spatial.KDTree(pts2)
kdtree.sparse_distance_matrix(kdtree2,0.4).toarray()

This is how to compute a matrix of distances between two KDTrees using the method sparse_distance_matrix of Python Scipy.

Read: Scipy Stats Zscore + Examples

Python Scipy Kdtree vs ckdtree

According to the most recent (v1.8) SciPy documentation, the functionally equivalent scipy.spatial.KDTree has taken the place of the deprecated scipy.spatial.cKDTree.

cKDTree is essentially equivalent to KDTree. Prior to SciPy v1.6.0, cKDTree offered superior performance and subtly different functionality but today the two names exist primarily for backward-compatibility reasons. If compatibility with SciPy < 1.6 is not an issue, prefer KDTree.

Python Scipy Kdtree leafsize

The method KDTree accepts a parameter leafsize that defines how many times the algorithm turns to brute-force methods, by default it is 10. Based on the leafsize method returns different results.

Let’s take an example by following the below steps:

Import the required libraries using the below code.

from scipy import spatial
import numpy as np

Generate data points using the method np.random.rand() and pass the data points to two kdtree with leafsize for one tree equal to 20 and the other equal to 10.

points = np.random.rand(20,3)

Tree1 = spatial.KDTree(points, leafsize=20)
Tree2 = spatial.KDTree(points, leafsize=10)

Find all points within the distance 0.2 of point 0.4 for both trees using the below code.

neighbors_1= Tree1.query_ball_point((0.4,0.3,0.2), r=2.0)
neighbors_2= Tree2.query_ball_point((0.4,0.3,0.2), r=2.0)

Check the result using the below code.

print(neighbors_1)
print(neighbors_2)

As we can see the result of both trees is different for the same query ball point parameter, This is due to the leafsize of the trees.

Read: Scipy Signal – Helpful Tutorial

Python Scipy Kdtree Slow

We have already talked about in the above subsection “Python Scipy Kdtree vs ckdtree” that ckdtree is better than kdtree in performance.

Let’s see with an example by following the below steps:

Import the required libraries using the python below code.

from scipy.spatial import KDTree, cKDTree
from itertools import combinations
from scipy.spatial.distance import cdist
import time
import numpy

Create data points using the below code.

points = [numpy.random.randn(100,2) for x in range(100)]

Use the ckdtree to find all the points using the method query_ball_points and also the time is taken by this method using the below code.

start = time.time()

c_trees = [cKDTree(x) for x in points]

for c_p1, c_p2 in combinations(c_trees,2):
    c_p1.query_ball_tree(c_p2,0.5,eps=1)

print("Time taken by ckdtree",time.time() - start)

Again same code with kdtree using the below code.

start = time.time()

kd_trees = [KDTree(x) for x in points]

for k_p1, k_p2 in combinations(kd_trees,2):
    k_p1.query_ball_tree(k_p2,0.5,eps=1)

print("Time taken by kdtree",time.time() - start)

From the output of both trees, we have concluded that the ckdtree is better in performance than the kdtree.

Also, take a look at some more Python SciPy tutorials.

• Python Scipy Eigenvalues
• Python Scipy Stats Kurtosis 
• Python Scipy Minimize
• Python Scipy Stats Skew
• Python Scipy Distance Matrix

So, in this tutorial, we have learned about the “Python Scipy KDTree” and covered the following topics.

• What is KDtree
• Python Scipy Kdtree Query
• Python Scipy Kdtree Query Ball Point
• Python Scipy Kdtree Query Pairs
• Python Scipy Kdtree
• Python Scipy Kdtree Query Ball Tree
• Python Scipy Kdtree Count Neighbors
• Python Scipy Kdtree Sparse Distance Matrix
• Python Scipy Kdtree vs ckdtree
• Python Scipy Kdtree Leafsize
• Python Scipy Kdtree Slow